Résumé
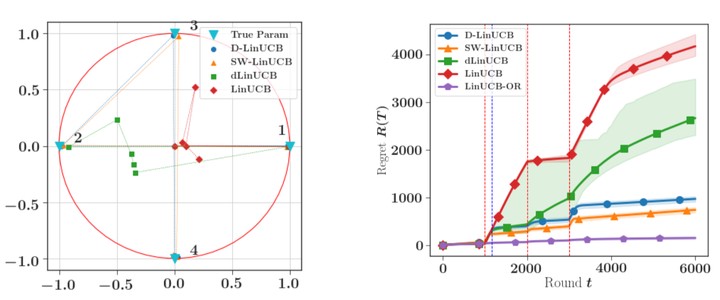
We consider a stochastic linear bandit model in which the available actions correspond to arbitrary context vectors whose associated rewards follow a non-stationary linear regression model. In this setting, the unknown regression parameter is allowed to vary in time. To address this problem, we propose DLinUCB, a novel optimistic algorithm based on discounted linear regression, where exponential weights are used to smoothly forget the past. This involves studying the deviations of the sequential weighted least-squares estimator under generic assumptions. As a by-product, we obtain novel deviation results that can be used beyond non-stationary environments. We provide theoretical guarantees on the behavior of DLinUCB in both slowly-varying and abruptly-changing environments. We obtain an upper bound on the dynamic regret that is of order $d^{\frac{2}{3}} B_T^{\frac{1}{3}} T^{\frac{2}{3}}$, where $B_T$ is a measure of non-stationarity ($d$ and $T$ being, respectively, dimension and horizon). This rate is known to be optimal. We also illustrate the empirical performance of DLinUCB and compare it with recently proposed alternatives in simulated environments.
Yoan Russac
Chercheur en Machine Learning
Je suis intéressé par le Machine Learning et plus particulièrement les méthodes d’apprentissage séquentiel.