Regret Bounds for Generalized Linear Bandits under Parameter Drift
Résumé
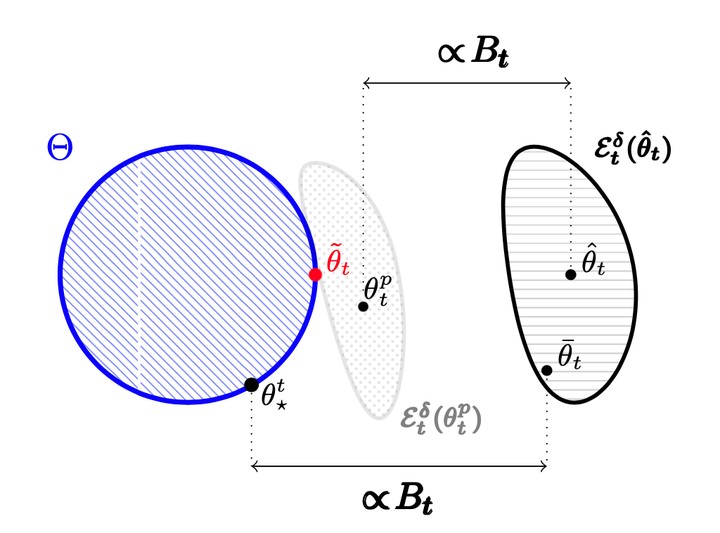
Generalized Linear Bandits (GLBs) are powerful extensions to the Linear Bandit (LB) setting, broadening the benefits of reward parametrization beyond linearity. In this paper we study GLBs in non-stationary environments, characterized by a general metric of non-stationarity known as the variation-budget or \emph{parameter-drift}, denoted $B_T$. While previous attempts have been made to extend LB algorithms to this setting, they overlook a salient feature of GLBs which flaws their results. In this work, we introduce a new algorithm that addresses this difficulty. We prove that under a geometric assumption on the action set, our approach enjoys a 0$(B_T^{\frac{1}{3}}T^{\frac{2}{3}})$ regret bound. In the general case, we show that it suffers at most a O($B_T^{\frac{1}{5}}T^{\frac{4}{5}}$) regret. At the core of our contribution is a generalization of the projection step introduced in Filippi et al. (2010), adapted to the non-stationary nature of the problem. Our analysis sheds light on central mechanisms inherited from the setting by explicitly splitting the treatment of the learning and tracking aspects of the problem.